
Nachweisgrenzen in der CCD-Technik
Eine
Untersuchung am Beispiel Europäischer Großteleskope
Wolfram Fischer
entstanden Febr. 2002 - Jan. 2003,
Layout überarbeitet Jan. 2025
Vorbemerkungen
Die optische
Nachweisbarkeit astronomischer Quellen wird durch zahlreiche Faktoren bestimmt.
Diese liegen im weitesten Sinne in den optisch-instrumentellen Gegebenheiten,
den Beobachtungsbedingungen, den Sensoreigenschaften und in der Natur des
Lichtes. Der physikalische Hintergrund dieses Themas ist einigermaßen komplex.
Schon wer sich im "Handbuch für Sternfreunde" den Formelwald zu den Abschnitten
Bildhelligkeiten und Grenzgrößen ansieht, wird, vor allem als Nichtfachmann, nur
schwer im Detail dessen Auswirkungen auf die Beobachtungspraxis nachvollziehen
können.
Das Europäische
Südobservatorium (ESO) entwickelte zur Beherrschung dieses Themenkreises,
nämlich zur Planung von Beobachtungen an Instrumenten ihrer Riesenteleskope das
Computerprogramm "Exposure Time Calculator" (ETC). Dieses Programm kann ebenso
von Außenstehenden über Internet (http://www.eso.org/observing/etc/)
genutzt werden. Es berechnet für das ausgewählte Instrument die
Belichtungszeiten, bzw. das Signal-zu-Rausch-Verhältnis, das bei einer
eingegebenen Grenzhelligkeit und Belichtung erreicht wird. Das Programm kann für
Direktaufnahmen (Punkt- oder Flächenobjekte) oder spektroskopische Aufnahmen
genutzt werden. Die für die Rechnungen eingesetzten mathematischen Formeln
finden sich unter
http://www.eso.org/observing/etc/doc/gen/formulaBook/etc.html
(Seite 2025 öffentlich nicht mehr erreichbar).
Für mich als Astroamateur bot sich hiermit in einmaliger Weise die Möglichkeit, quasi im
Experiment, durch exakte Modellrechnungen, Sachverhalte in Grenzgrößenfragen zu
erkunden und eigene Vorstellungen zu überprüfen.
Die hier dargelegten Untersuchungen beziehen sich auf Leistungsparameter dreier
europäischer Großteleskopsysteme, geben aber zugleich Einblicke in allgemeine
Zusammenhänge.
Allgemeines
Geht es darum, die
Grenzgrößenentwicklung einer Aufnahme mit fortschreitender Belichtung zu
prognostizieren, liegt der laienhafte Gedanke nahe, dass sich die Intensitäten
der schwächsten abgebildeten Sterne linear mit dem Belichtungsfaktor entwickeln.
In der Fgtografie bremst bekanntlich das Schwarzschildverhalten der Emulsionen,
nicht jedoch in der CCD-Astronomie. Man könnte also erwarten, dass nach 10facher
Belichtung auch 10mal schwächere Sterne erreichbar sind.
Ebenso im Instrumentenvergleich. Sollten sich hier die Nachweisgrenzen nicht unmittelbar
aus den unterschiedlichen Abbildungsintensitäten herleiten können, die sich bei Sternen (Punkthelligkeiten) primär aus der Größe der wirksamen Objektivfläche
ergeben? Der Grenzgrößenverlauf zweier Aufnahmen mit
unterschiedlich großen Objektiven sollte also im Abstand des Objektivflächenverhältnisses
parallel verlaufen, (z.B. doppelte Öffnung gleich 1,5 mag
Grenzgrößenunterschied).
Ebenso wie sich die Abbildungsintensität von Sternen
mit wachsender Öffnung mehrt, steigert sich diese mit wachsender Bildschärfe
(Fokussierung, Nachführung, Abbildungsgüte, Seeing, adaptive Optik).
Auch bei doppelter Bildschärfe vervierfacht sich die Abbildungsintensität und 1,5 mag
Reichweitengewinn scheinen logisch.
Dass all diese Erwartungen in der Praxis
nicht eintreten, liegt im Wesentlichen am Einfluss der Hintergrundhelligkeit des
Himmels
(siehe Kasten 1)
und an den
statistischen Schwankungen der Photonenzahlen von Objekt und Hintergrund.
Kasten 1
|
Helligkeit des
Himmelshintergrundes bei Neumond unter idealen irdischen Bedingungen und
verschiedenen Farbbereichen in mag/arcsec2 [1]. (Grundlage aller im
Beitrag durchgeführten ETC-Rechnungen.)
U
B
V
R
I
Z
22,0
22,7
21,8
20,9
19,9
18,8 |
Natürlich kommt dies besonders bei lichtschwachen
Objekten (und das betrifft per definitionem die Grenzhelligkeit!) zum Tragen, wenn z.B. ein Stern zur
Photonenzahl des Himmels nur noch wenig beiträgt. Dies alles führt dazu, dass
Schwärzungs-, bzw. Ladungszuwächse und Abbildungsintensitätsverhältnisse sich nicht generell proportional in den Grenzgrößen
niederschlagen.
So ist der mit der Belichtung voranschreitende Grenzgrößenzuwachs ein erstaunlich dynamisches Phänomen. Für dieses
Zustandekommen und die sich hier aufaddierenden Effekte, z.B. für das
Ausleserauschen oder den Dunkelstrom eines CCDs, hat man kein unmittelbares
"Gefühl" und ist auf eine formelmäßige Behandlung angewiesen. Genau das macht
der "Exposure Time Calculator" der ESO.
Ich möchte an dieser Stelle die Informatiker unter den Sternfreunden aufrufen, ein ähnliches Programm, anwendbar
für beliebige Instrumente, CCDs und zusätzlich für das Aufsummieren von
Einzelaufnahmen zu entwickeln. Auch wenn der Amateur nicht überall exakte Werte
eingeben kann, etwa über die Helligkeit des Himmelshintergrundes am Beobachtungsort oder über das aktuelle Reflexionsvermögen seiner Spiegel, es
ließen sich dennoch viel genauere Auskünfte, über die eigenen instrumentellen
Möglichkeiten und eine Vielzahl von Zusammenhängen, gewinnen. Es würde
zweifellos eine bedeutende und interessante Angebotslücke geschlossen! Der
vorliegende Beitrag steht dafür.
Ausbelichtung und
Signal-Rausch-Verhältnis
Bekanntlich sind in der klassischen Fotografie die Belichtungszeiten durch die
Helligkeit des Himmelshintergrundes limitiert. Die größte Reichweite (Tiefe),
bzw. das beste Signal-zu-Rausch-Verhältnis wird bei einer noch geringen
Schwärzung des Himmelshintergrundes erreicht.
Dies ist eine Eigenart der
fotografischen Emulsionen! Man spricht hier von ausbelichteten Aufnahmen.
Wird länger belichtet, verringert das zunehmende "Störsignal" des Hintergrundes
die Objektinformationen, bis zur totalen Auslöschung!
Auch wenn die CCD-Technik mit der klassischen Fotografie
auch hier durchaus Gemeinsamkeiten aufweist, existieren signifikante
Unterschiede. Die Signal-zu-Rausch-Theorie, der Schlüssel zum Verständnis, ist
in der CCD-Technik, auf Grund der Liniarität und einfacher Messmöglichkeiten
leicht anwendbar.
Während der Belichtung setzen die registrierten Photonen in den CCD-Pixeln durchschnittlich
1 bis 2 Elektronen frei. Eine elektrische Ladung entsteht. Der Quantennatur des
Lichtes zufolge gibt es eine bestimmte Wahrscheinlichkeit, wie viele der
aufgefangenen Photonen von der Quelle (S = Signal) stammen, bzw. Rauschen (N =
engl. noise) sind. Diese Unsicherheit ist statistisch N = √S. Interessiert
man sich für die schwächsten überhaupt erreichbaren Objekte, gilt es, von den
astronomischen Gegebenheiten her primär das dominante Störsignal des
Himmelshintergrundes (Nh) zu berücksichtigen. Aus den detektierten Photonenzahlen
der Quelle S und Nh berechnet sich das Signal-zu-Rausch-Verhältnis (S/N) in erster Näherung aus:
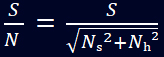 Vereinfacht bedeutet das nichts anderes als:
Vereinfacht bedeutet das nichts anderes als:
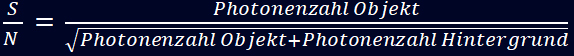 (1)
(1)
Dabei werden Ausleserauschen und
Dunkelstromrauschen nicht beachtet. Nähere Informationen zu diesem Thema finden
sich z.B. unter [2].
Als unterste Nachweisgrenze einer Quelle gilt S/N = 3. Fachleute benutzen zum sicheren
Nachweis eines Sterns S/N = 5, bei Spektren mindestens 10. Da ein CCD-Pixel im
Prinzip nach doppelter Belichtung die doppelte Ladung aufbaut, lässt sich aus
Formel 1 in erster Näherung ableiten, dass das S/N-Verhältnis mit dem Quadrat
der Belichtung anwächst.
Also um den S/N-Wert um den Faktor 2 zu steigern, muss 4mal
länger belichtet werden. Daraus folgt, dass in der CCD-Technik sich mit
wachsender Belichtung das Signal-zu-Rausch-Verhältnis stetig verbessert.
Dieser Eigenschaft und der hohen Quanteneffizienz verdanken CCD-Aufnahmen ihre
enorme Reichweitenüberlegenheit. Sie tritt besonders krass zu Tage, wo
fotografische Aufnahmen aufgrund eines zu kleinen Öffnungsverhältnisses nicht ausbelichtet werden können. Aber selbst ausbelichtete Fotografien können von
einzelnen CCD-Aufnahmen in ihrer Reichweite ohne weiteres um 3 oder 4
Größenklassen übertroffen werden!
Es gibt hier im klassisch fotografischen Sinne
eben
keine Ausbelichtung.
Grenzgrößenverlauf und Sättigungszeit
Obwohl in der CCD-Astronomie nicht von
Ausbelichtung gesprochen werden kann, werden dennoch auch hier die
Einzelbelichtungen durch den Himmelshintergrund, (bei Amateurkameras spielt auch
der Dunkelstrom eine bedeutende Rolle), limintiert, da die CCD-Pixel über kurz
oder lang die Ladungssättigung (full well capacity) erreichen. Die Bilder sind
dann ein weißer Fleck. Bis zu diesem Punkt jedoch steigen
die Grenzgrößen prinzipiell an! In
der Stadt kann der Himmelshintergrund bei f/10, je nach Kamera und
Kühltemperatur variierend, größenordnungsmäßig bereits nach 40s und außerhalb
nach 10min zur Sättigung führen.
Mit dem Instrument FORS 2 (Focal
Reducer / low dispersions Spektrograph, f/3,1) an einem 8,2 m Very
Large Telescope (VLT) auf dem Cerro Paranal, führt allein der Himmelshintergrund
(ohne Filter, Binning 2x2, alle Rechnungen in diesem Beitrag
stets mit Dunkelstrom und Ausleserauschen) unter idealen Bedingungen auch
schon nach ca. 470s (7min 50s) zur totalen Sättigung.
Die viel gepriesene Linearität von
CCD-Detektoren bedeutet nicht, dass auch die Grenzgrößen linear mit der
Belichtung wachsen. Mit Hilfe des ETC der ESO lässt sich veranschaulichen, dass,
obwohl die Pixelladungen nahezu linear mit der Belichtung zunehmen, der
Grenzgrößengewinn immer langsamer wird.
Um das erforderliche Signal-zu-Rausch-Verhältnis für immer schwächere Quellen zu erreichen, muss,
durch das übermäßig anschwellende Hintergrundsignal, immer länger belichtet werden. Die Diagramme 1 und 2 zeigen dieses
Verhalten am Beispiel von FORS 2. Farbige Kurven im Diagramm 1 kennzeichnen das
Leistungsvermögen des Instruments bei Sternen und Nebeln und von Spaltspektren
niedrigster Dispersion. Die schwarze gestrichelte
Kurve im Diagramm 1 zeigt den Grenzgrößenverlauf der stattfände, wenn bei
doppelter Belichtungszeit stets doppelt so schwache Sterne (+0,752575 mag)
nachweisbar wären. Ausgangspunkt der Berechnung war 10-4%
Sättigungszeit (blaue Kurve) und S/N=5.
Will man von einer absoluten
Nachweisgrenze von S/N=3 ausgehen, so sind zu den Helligkeitsangaben +0,555 mag
dazu zu addieren.
Die auf der X-Achse aufgetragene Sättigungszeit, von 100%
rückgerechnet, ergibt, dass beispielsweise bei 1% dieser Zeit
der Chip bereits etwas mehr als 1% gesättigt ist.
Mit anderen Worten, mit
voranschreitender Belichtung verringert sich bei CCDs der Ladungszuwachs
geringfügig! Dies ist ein Beleg dafür, dass die
Postulierung der Linearität des Ladungszuwachses die Verhältnisse nur ungefähr
beschreibt.
Da in der Praxis Einzelbelichtungen in
der Regel nicht länger als maximal ein oder zwei Stunden belichtet werden,
wurden im Diagramm die Grenzgrößen für 2 Stunden gegeben. Darüber hinaus wird
mit aufaddierten, bzw. gemittelten Teilbelichtungen gearbeitet.
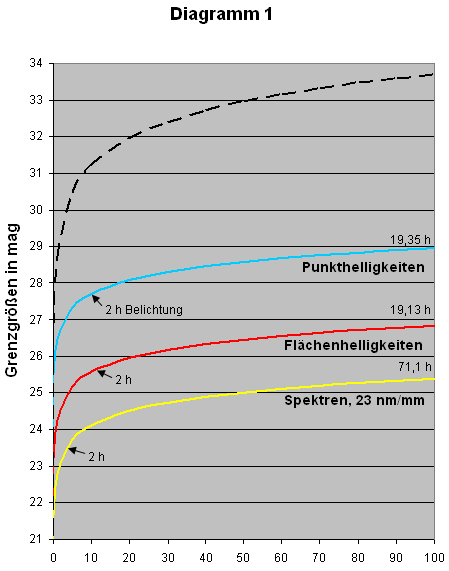
Diagramm 1:
Grenzgrößen und Sättigungszeiten (in %) für Sterne, Nebel und Spektren am 8,2 m VLT mit dem Instrument FORS 2
(11000 K Farbtemperatur, Seeing 0,65", z=0, Bessel B-Filter,
B-Band, Binning 1x1, S/N=5, Flächenhelligkeiten in m/arcsec2, Spaltspektren niedrigster Dispersion mit 23 nm/mm, Spaltbreite 0,4", Binning 2x2, R-Band, S/N=10, bezogen auf eine zentrale Wellenlänge von 715 nm).
Am rechten Rand die 100%-Sättigungszeiten. Die schwarz gestrichelte Kurve zeigt den Verlauf, der bei linear mit der Belichtung anwachsenden Sterngrenzgrößen entstünde.
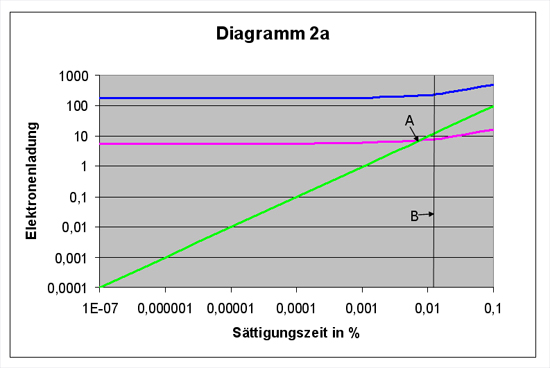
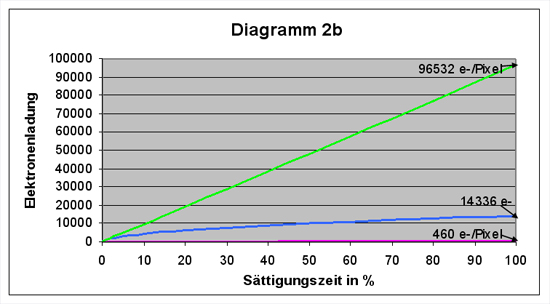
Diagramme 2:
Ladungszuwachs im Detektor von FORS 2 (8,2 m-VLT) erzeugt durch den Himmelshintergrund (ETC-Rechnungen wie für Sterne in Diagramm 1)
Die Diagramme 2 veranschaulichen
den Elektronenladungszuwachs im Detektor von FORS 2 durch gerade nachweisbare
Sterne (S/N=5, entsprechend der blauen Kurve im Diagramm 1) plus
Himmelshintergrund.
Die grüne Linie zeigt den Anstieg durch die
Hintergrundhelligkeit. Blau ist die Linie, die den Ladungszuwachs allein durch
den Stern, die Summe sämtlicher von ihm beleuchteter Pixel (85), auch PSF area
genannt (PSF = Point Spread Function, Punktverbreiterungsfunktion), beschreibt.
Die rote Linie weist auf die Ladung des hellsten Pixels eines "Grenzsterns" hin.
Im
Diagramm 2a wird der kurze Belichtungsbereich dargestellt. Während die
Hintergrundhelligkeit mit einem annähernd linearen Ladungszuwachs stetig
zunimmt, ist der Ladungsverlauf schwächster nachweisbarer Sterne im ultrakurzen
Bereich bemerkenswert. Obwohl, wie später gezeigt wird, gerade hier der
Grenzgrößengewinn am höchsten ist, nimmt die Ladung, selbst über eine um 5
Zehnerpotenzen verlängerte Belichtung hinweg, kaum merklich zu.
Es fragt sich,
was den Grenzgrößenzuwachs eigentlich ausmacht?
Diagramm 2b zeigt anschaulich, wie mühsam die schwächsten nachweisbaren
Sterne gegen die machtvoll zur Sättigung strebende Hintergrundhelligkeit
anrennen müssen.
Rechts im Diagramm die Ladungswerte im
Augenblick der Detektorsättigung, durch Objekt und Hintergrund.
Mit wachsender Belichtung wird
die Dynamik einer Aufnahme, die Fähigkeit
Helligkeitsunterschiede darzustellen, zwischen dem anschwellenden
Hintergrundsignal und der drohenden Sättigung platt gequetscht. Das Ergebnis sind
immer hellere, kontrastärmere Bilder.
Nach 50% Sättigungszeit ist kaum noch ein
weiterer Reichweitengewinn erzielbar. Noch längere Belichtungen sind, durch die
immer drastischere Reduzierung der Dynamik, kaum sinnvoll. Gute CCD-Einzelaufnahmen werden in der Regel nur wenige Prozent der Sättigungszeit
belichtet. Aus der Sicht "schöner" Bildresultate sollte also ein bestimmter
Belichtungsrahmen nicht überschritten werden.
Das ist nicht anders als in der herkömmlichen Fotografie.
Grenzgrößengewinn und
vervierfachte Belichtungen
Aus Formel 1 lässt sich in erster Näherung die Erkenntnis
gewinnen, dass für CCD-Kameras das S/N-Verhältnis mit dem Quadrat der Belichtung
anwächst. Dies bedeutet nichts anderes, als dass sich nach 4facher Belichtung
die Reichweite verdoppeln sollte (+0,752575 mag). Die Überprüfung dieses
Rechenschemas mit Hilfe des ETCs ist Inhalt von Diagramm 3. Verglichen werden
hier das 8,2 m VLT mit FORS 2 (f/3,1-rote Kurve)
und das 3,6 m ESO New Technology Telescope (NTT) in La
Silla mit SUSI 2
(Superb Seeing Imager-2,
f/11-schwarze Kurve).
Die gelben Messpunkte auf der roten Kurve markieren
den Ort einer jeweils um das Vierfache verlängerten Belichtung. Die Y-Achse
zeigt an, welcher Grenzgrößengewinn sich von einem Messpunkt zum vorherigen
ergibt. Aus den abgerundeten Grenzgrößenangaben unter den Messpunkten kann dies
auch leicht nachvollzogen werden. Oberhalb der Kurve steht meist die gerundete
Belichtungszeit für das VLT in Sekunden. Die X-Achse ist logarithmisch gestaucht
und macht dadurch den Verlauf im ultrakurzen Belichtungsbereich anschaulich.
Es ist ein Belichtungsbereich von 10-7% bis 100% Sättigungszeit
angezeigt. Es verbergen sich dahinter beim VLT 4,9124 x 10-6s bis 4912,4s, beim
NTT 5,07 x 10-5s
bis 50739s (rund 14 Stunden).
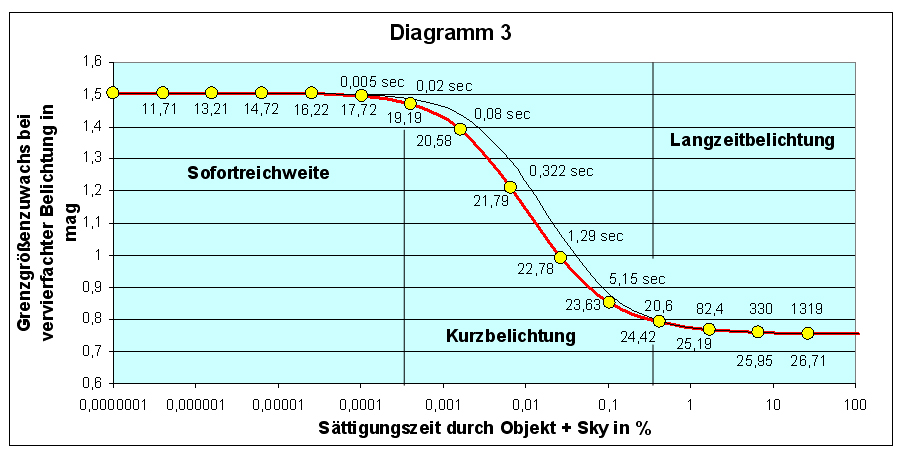
Diagramm 3:
Grenzgrößenzuwachs bei vervierfachten Belichtungszeiten, rote Kurve und
Zahlenangaben gültig für FORS 2 am
8,2 m VLT (f/3,1,
Einstellungen: Punkthelligkeiten mit 11000 K Farbtemperatur,
Seeing 0,65", z=0, Bessel V-Filter, V-Band, Binning 2x2, S/N=5),
schwarze Kurve gültig für SUSI 2 am 3,6m NTT (f/11,
Filter V#812,
sonst gleiche Einstellungen).
Die Angaben im Diagramm
beeindrucken natürlich durch die unglaubliche Sofortreichweite, die sich durch
die gewaltige Abbildungsintensität der 51,2m2 Öffnungsfläche des VLTs
(plus CCD-Empfindlichkeit) aufbaut.
Wie sich zeigt, ist im ultrakurzen
Belichtungsbereich der Grenzgrößenzuwachs tatsächlich linear, 4fache Belichtung
= 4mal schwächere Sterne (+1,505 mag).
Bereits ab 0,005 Sekunden wird der
Einfluss des Himmelshintergrundes deutlich, der zunehmend den Grenzgrößengewinn
bremst.
Im Bereich der Kurzbelichtung, hier bis etwa 20 Sekunden, stürzt die
Kurve förmlich ab, um sich dann ganz allmählich dem oben aufgestellten
Zusammenhang, 4fache Belichtung = doppelte Grenzgröße stark zu nähern.
Von 20,6s
bis zur Sättigung würde die Anwendung dieses einfachen Rechenschemas eine
maximal 0,03 mag zu geringe Grenzgröße ergeben.
Im Bereich von Langzeit-CCD-Aufnahmen ist also die Vorstellung, dass eine 4fache Belichtung die
doppelte Grenzgröße bringt, durchaus richtig!
Die Intensität der schwächsten
nachweisbaren Sterne (IST) wächst demnach bei Langzeitaufnahmen mit
der Wurzel des Belichtungsfaktors (Bf):
(2) IST = √ Bf
Umrechnung von IST
in Größenklassklassen: mag = lgIST: 0,4
Um eine Größenklasse tiefer zu kommen, muss
demnach 6,31mal länger belichtet werden!
Meine hier verwendete Dreiteilung
(Sofortreichweite, Kurzbelichtung, Langzeitbelichtung) kennzeichnet
charakteristische Kurvenabschnitte, die etwa zwischen 0 bis 0,0004%, 0,0004% bis
0,4% und zwischen 0,4 bis 100% Sättigungszeit liegen. Im Langzeitbereich beträgt
der prinzipielle Belichtungsfaktor 100 : 0,4 = 250, was einem hier möglichen
Grenzgrößenzuwachs von 3 mag gleich kommt.
Die übergelegte schwarze Kurve des NTTs
bestätigt den allgemein gültigen Charakter des Verlaufs. Hauptsächlich wegen des
viel kleineren Öffnungsverhältnisses (f/11) verbirgt sich hinter der schwarzen
Kurve die rund 10fache Belichtungszeit.
Um beispielsweise der Sättigungszeit des Messpunktes 20,6s zu entsprechen, muss
am NTT 212,8s belichtet werden. Der Dunkelstrom an diesem Instrument wird
übrigens mit lediglich 0,1 e-/Pixel/Stunde angegeben und ist von sehr geringem
Einfluss.
Zu erkennbaren
Abweichungen im Kurvenverlauf kommt es lediglich im Bereich der Kurzbelichtung.
Die Einflussnahme des Himmelshintergrundes tritt durch das kleine
Öffnungsverhältnis langsamer in Erscheinung, wovon der Reichweitenzuwachs bei
Sternen profitiert - mehr dazu im nächsten Abschnitt. Aber auch Unterschiede in
den Transmissionseigenschaften der Filter und der spektralen Empfindlichkeit der
CCD-Detektoren nehmen hier Einfluss.
Öffnung
und Reichweite
Bekanntlich ist die
Abbildungsintensität von Punktlichtquellen (Sternen) primär von der wirksamen
Teleskopöffnung und ihrer Verteilung im Fokus abhängig. Wie sich diese
Abhängigkeit im Grenzgrößenverlauf dreier unterschiedlich großer Teleskope (8,2m
VLT mit FORS 2, 3,6m NTT mit SUSI 2 und ESO/MPG 2,2m Telescope f/5,9 Instrument
WFI, Wide Field Imager) tatsächlich auswirkt, offenbaren
die Diagramme 4a und 4b. Diese zeigen den relativen Verlauf gegenüber einem 8,2m
VLT (rot). Die Werte wurden am ETC für alle Teleskope mit gleichen
Einstellungen (Seeing, Binning 2x2, ect.) und ohne Filter gerechnet. Die 100%ige
Sättigungszeit, Endpunkt jeder Kurve, bezieht sich auf Objekt plus Hintergrund.
Die wirksamen
Öffnungsflächen der Teleskope betragen 51,2m2, 8,9m2
und 3,8m2. Unter Annahme eines gleichen Seeings (0,65") und gleicher
Effizienz beträgt der Unterschied in der Abbildungsintensität bei Sternen
relativ zum VLT 1:5,753, bzw. 1:13,474. In Grenzgrößen übertragen bedeutet dies
-1,9 mag, bzw. -2,82 mag.
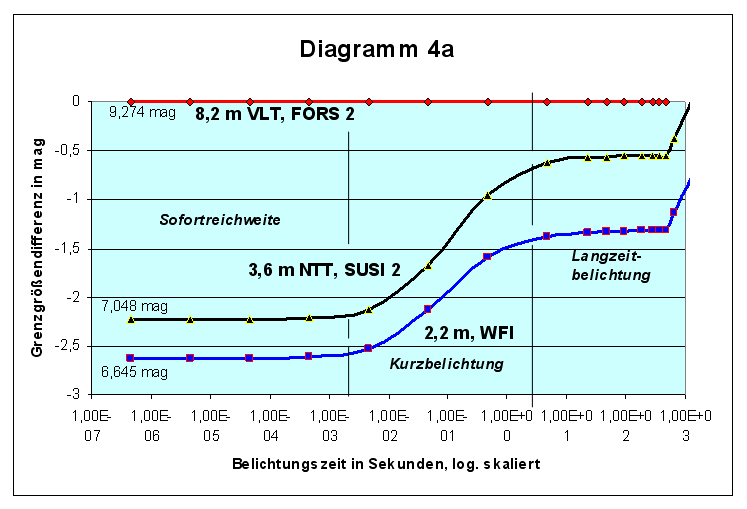
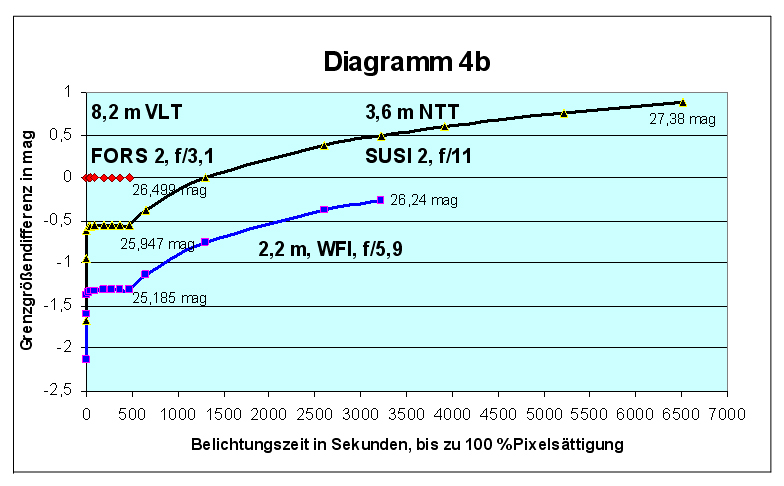
Diagramme 4:
Grenzgrößenentwicklung des 3,6m-NTT und des ESO/MPG 2,2m-Teleskops
relativ zum 8,2m VLT (rot) (gleiche ETC-Einstellungen für alle
Teleskope).
Dieser durch die Öffnung bedingte
Grenzgrößenabstand findet sich, vom Himmelshintergrund noch
unbeeinflusst, nur im Moment des Belichtungsbeginns (Sofortreichweite).
Das NTT bleibt hier 0,326 mag hinter diesem Wert zurück. Das 2,2m
Teleskop liegt 0,195 mag darüber. Grund dafür sind die unterschiedlichen
instrumentellen Lichtverluste und Detektorempfindlichkeiten.
Bemerkenswert ist nun, wie im Bereich der Kurzbelichtung dieser
Grenzgrößenabstand, vor allem des 3,6m NTT, sich erheblich verringert.
Danach schließt sich ein fast paralleler Langzeitbelichtungsbereich an.
Wenn FORS 2 am 8,2m VLT nach 467,5s die Ladungssättigung erreicht,
liegen die Grenzgrößen der anderen Teleskope nur noch 0,55 mag, bzw.
1,31 mag dahinter, als hätten sich ihre Öffnungsflächen auf 30,8m2,
bzw. 15,3m2 vergrößert. Das
Kuriose daran ist, dass hierfür letztlich die Effizienz und
Leistungskraft des 8,2m Teleskops erheblich selbst beiträgt.
Während die
Abbildungsintensität von Punkthelligkeiten mit dem Quadrat der wirksamen
Öffnung wächst, entwickelt sich die Abbildungsintensität von
Flächenhelligkeiten, so auch des Himmelshintergrundes, mit dem Quadrat
des Öffnungsverhältnisses. Wir haben es hier mit zwei unterschiedlichen
und getrennt wirkenden Abbildungsgesetzen zu tun.
FORS 2
am 8,2m VLT ist mit einem Öffnungsverhältnis von f/3,1 überaus
lichtstark. Gegenüber SUSI 2 am NTT (f/11) bildet es den
Himmelshintergrund 12,6mal heller, gegenüber WFI am 2,2,m Teleskop
(f/5,9) 3,6mal heller ab.
Im Bereich der Kurzbelichtung wird beim VLT, durch die viel höhere
Intensität des Himmelshintergrundes, das Signal-zu-Rausch-Verhältnis
wesentlich stärker gebremst. Im Ergebnis stürzen die Kurven der anderen
Teleskope auf das VLT zu.
Im Langzeitbereich ist dagegen der
Zugewinn an Signal-zu-Rausch-Verhältnis für alle Teleskope und
Öffnungsverhältnisse offensichtlich annähernd gleich. Den gravierendsten
Unterschied im Langzeitbereich zeigt Diagramm 4b. Die lichtschwächeren
Teleskope müssen, bzw. können erheblich länger belichten. Im Ergebnis
bleibt das 2,2m Teleskop bei 100% Sättigungszeit hinter dem 8,2m VLT
rechnerisch lediglich 0,26 mag zurück. Das 3,6m NTT übertrifft, nach
13,9facher Integrationszeit das VLT sogar um 0,88 mag, also um mehr als
das Doppelte. Demnach ist bei gleicher Auflösung (Seeing-begrenzt) und
von sättigungsnahen CCDs aus beurteilt, ein unmittelbarer Zusammenhang
zwischen Öffnung und Grenzgröße nicht mehr erkennbar!
Dennoch sollte man nicht aus dem
Auge verlieren, dass der Einsatz größerer Teleskopöffnungen zur
Erzielung tiefer Direktaufnahmen effektiver ist. Auch wenn die
Detektorsättigung eher drohen sollte, lassen sich durch Addition
mehrerer Aufnahmen (siehe unten) extreme Grenzgrößen deutlich schneller
erzielen. Allerdings verspricht der Einsatz riesiger Optiken erst unter
Weltraumbedingungen, oder zumindest mit adaptiven optischen Systemen,
einen grundlegenden Informationsgewinn. Die Auflösungsüberlegenheit und
im Weltraum ein, je nach Spektralbereich, 6 bis 15mal dunklerer
Himmelshintergrund kämen zum Tragen.
Weshalb sich allerdings die
Berechnungen des ETCs mit den in der Literatur und im Internet für das
8,2m VLT verbreiteten deutlich höheren Grenzgrößenangaben nicht
vertragen, z.B. 29. Größe in 30 Minuten bei 0,5" Seeing und V-Filter
[3], darauf habe ich bis heute keine Antwort erhalten.
Bildschärfe und
Grenzgröße
Natürlich wird Sternlicht, das auf
den halben Durchmesser gebündelt wird, (etwa durch Fokussierung, Seeing
oder adaptive Optik), 4mal heller, weil es nur ¼ der vorherigen
Fläche bescheinen muss. Dieser Umstand korreliert aber nicht mit den
erzielbaren Sterngrenzgrößen. Der Grund liegt in der Beschaffenheit der CCD-Detektoren, in der Helligkeit des Himmelshintergrundes, aber vor
allem im Ausleserauschen des CCDs und
in den statistischen Schwankungen der Photonenzahlen von Stern und
Hintergrund.
Die CCD-Pixel sind meist
quadratisch, (beim 8,2m VLT, FORS 2, besitzen die Pixel eine Kantenlänge
von 24μm = 0,125"/Pixel) und deren beleuchtete Anzahl skaliert
nicht exakt mit dem Seeing, das idealerweise kreisförmige Sterne
produziert. Tabelle 1 macht die Zusammenhänge deutlich. Die Werte wurden
wieder mit Hilfe des ETCs für FORS 2 berechnet. (Einstellungen:
Punkthelligkeit, 11000 K, Bessel V-Filter, Binning 1x1, S/N=5,
Grenzgröße bezogen auf 50% Sättigungszeit durch Objekt+Sky.)
Grundlage der sich halbierenden Seeing-Werte, war die Winkelgröße
zentraler Beugungsscheibchen eines idealen 8,2m Teleskops (0,0357" bei
λ=550nm).
Tabelle 1 zeigt, wie der
entstehende Grenzgrößengewinn mit dem Verhältnis der beleuchteten
Pixelzahlen einhergeht. Vierteln sich diese sehr
genau, steigt die Sterngrenzgröße um 0,75 mag. Bei relativ
wenigen beleuchteten Pixeln ist die Abweichung von dieser Regel noch
klein. Im Bereich der Auflösungsgrenze des CCDs verändern sich die
Pixelzahlen kaum noch. Der Reichweitenzuwachs wird immer geringer.
Trifft das Sternlicht nur noch ein einzelnes Pixel, führt eine weitere
Abbildungsschärfung, trotz Intensitätssteigerung, zu keinem weiteren
Grenzgrößenzuwachs.
Tabelle 1
| Seeing |
Grenzgröße in mag |
Gewinn in mag |
beleuchtete Pixel |
Verhältnis der Pixelzahlen |
| 36,5568" |
23,45306 |
0,75249 |
268700 |
268700 : 67175 = 1 :
4,0000 |
| 18,2784" |
24,20555 |
0,75240 |
67175 |
67175 :
16794 = 1 : 3,9999 |
| 9,1392" |
24,95795 |
0,75215 |
16794 |
16794 :
4199 = 1 : 3,9995 |
| 4,5696" |
25,71010 |
0,75173 |
4199 |
4199 : 1050 = 1 : 3,9990 |
| 2,2848" |
26,46183 |
0,75011 |
1050 |
1050 : 263 = 1 : 3,9924 |
| 1,1424" |
27,21194 |
0,74770 |
263 |
263 : 66 = 1 : 3,9848 |
| 0,5712" |
27,95964 |
0,73116 |
66 |
66 : 17 = 1 : 3,8823 |
| 0,2856" |
28,69080 |
0,65620 |
17 |
17 : 5 = 1 : 3,4 |
| 0,1428" |
29,34700 |
0,49140 |
5 |
5 : 2 = 1 : 2,5 |
| 0,0714" |
29,83840 |
0,37640 |
2 |
2 : 1 = 1 : 2 |
|
0,0357" |
30,21480 |
0 |
1 |
1 : 1 = 1 : 1 |
| 0,01785" |
30,21480 |
0 |
1 |
1 : 1 = 1 : 1 |
Binning und Reichweite
"Binning" bedeutet "zusammenfassen", im englischen wörtlich
"eintüten" (engl. von bin: Behälter). Bereits in den in diesem Beitrag
verwendeten Einstellungen für die ETC-Rechnungen begegnete uns Binning
1x1 und 2x2. Bei Binning 1x1 ist ein Pixel ein Bildpunkt. Bei 2x2 wird
hingegen ein Quadrat von vier benachbarten Pixeln, bei 3x3 ein Quadrat
von 9 benachbarten Pixeln gemeinsam als ein Bildpunkt ausgelesen. Dabei
verschlechtert sich möglicherweise die Auflösung der Aufnahmen,
zumindest aber ihre Vergrößerungsfähigkeit. Positiv an diesem
"Zusammenfassen" ist, dass sich das empfangene Signal aufaddiert, also
verstärkt, ohne dass sich dabei etwas am Ausleserauschen ändert.
Die Empfindlichkeit des CCDs steigert sich also
drastisch. Dies gilt vor allem bei flächenhaften Objekten (leider
auch beim Himmelshintergrund), wo alle gemeinsam ausgelesenen Pixel
gleichmäßig beleuchtet werden.
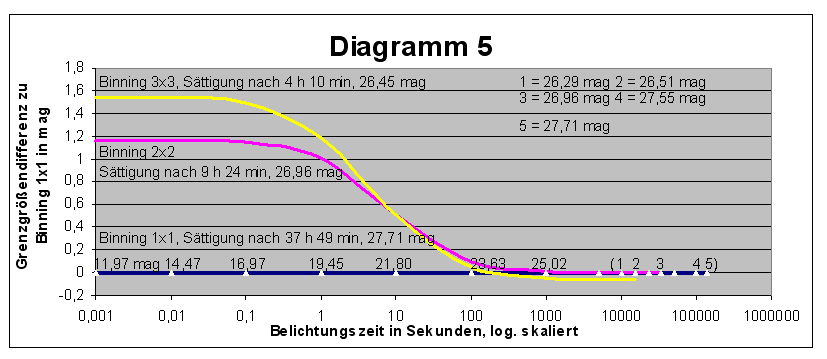
Wie sich dies auf die erzielbaren Sterngrenzgrößen auswirkt zeigt
Diagramm 5. Die Kurvenwerte wurden hier für das ESO/MPG 2,2m Telescope,
Instrument WFI mit folgenden Einstellungen bestimmt: Punkthelligkeiten,
11000K, Filter #843V, Seeing 0,65", S/N=5.
Es wird deutlich, dass im Bereich der Sofortreichweite und
Kurzbelichtung der zu größeren Pixeln zusammengefasste CCD-Chip, dank
der höheren Empfindlichkeit, wesentlich schwächere Sterne erreicht.
Diese Überlegenheit schwindet jedoch im Bereich weniger Sekunden, da der
Einfluss des Himmelshintergrundes ungleich ist. Im praktikablen
Langzeitbereich, ab etwa 100 Sekunden Belichtung, liefern alle drei Binningeinstellungen annähernd adäquate Grenzgrößen. Bemerkenswert ist, das die relativ geringe
Empfindlichkeit von Binning 1x1, durch die sehr späte Sättigung des
Chips das prinzipielle Erreichen geringster Grenzhelligkeiten
ermöglicht.
Addierte Einzelaufnahmen und Reichweite
Das Aufaddieren mehrerer CCD-Aufnahmen, also das Stückeln einer
Belichtung, ist eine beliebte Lichtsammelmethode. Sie verhindert das
Überlaufen heller Objekte (blooming), jedoch summiert sich das
Ausleserauschen. Eine drastische Reduzierung der Dynamik, durch
Hintergrund und Dunkelstrom, kann durch Subtraktion ihrer Ladungswerte
vermieden werden. Treffer kosmischer Höhenstrahlung (sog. "cosmics",
oft aber erzeugt durch radioaktive Zerfallsprozesse
im umliegenden Gestein)
lassen sich eliminieren. Aufnahmen, unter günstigem Seeing entstanden,
können ausgesucht und zu einem optimalen Bild kombiniert werden. Diese
Methode wird gern benutzt, um Nachführproblemen aus dem Weg zu gehen,
z.B. bei fehlendem Leitstern oder schlechter Montierung. Mehrere
CCD-Kameras der Firma SBIG ermöglichen dies über den Modus "Traccum-Accumulate",
wobei die Einzelbelichtungen, über eine spezielle Software
rückzentriert, mit Dunkelbildabzug zu einem Bild kombiniert, automatisch
ausgegeben werden.
Zunächst mag es wundern, dass viele Aufnahmen vereint etwas zeigen
sollen, was eine Einzelne nicht vermag. Schließlich ist Null plus Null gleich Null.
Tatsächlich gibt es
aber eine Wahrscheinlichkeit für die Registrierung von Photonen beliebig
schwacher Quellen, und dass wir ein Objekt auf einer Einzelaufnahme
nicht erkennen können, bedeutet nicht, dass von ihm kein Photon
empfangen wurde. Es muss nur eine genügende Anzahl von ihnen gezählt
werden, damit diese sich gegen das Rauschen durchsetzen. Von daher ist
es gleichgültig, ob eine Belichtung gestückelt wird oder nicht.
Dass sich hiermit tatsächlich ungewöhnliche Reichweiten erzielen
lassen, wurde mit dem berühmten Hubble-Deep-Field eindrucksvoll gezeigt.
10 Tage lang sammelte das Hubble-Teleskop im Dezember 1995 mit seiner
damaligen Kamera WFPC2 (Field-/Planetary Camera 2, f/13) Licht von einem
einzigen, nur 2′ großen Bildfeld. 342 Einzelaufnahmen
entstanden in 4 Farbbereichen, von denen man bisher 276 verarbeitete.
Die drei Grundfarben wurden insgesamt je 35 Stunden und das UV-Band 50
Stunden belichtet. Mit 30m wurde eine Traumgrenzgröße
erreicht!
Aber auch Amateure versuchten sich mittlerer Weile mit tiefen
Feldern. Der King of the Deep Sky wurde 1998 der kanadische
Astroamateur Paul Boltwood, der mit einer selbst gebauten CCD-Kamera, an
einem 16 Zoll-Newton (f/4,78) mit 601 Einzelaufnahmen ein Feld insgesamt
20 Stunden belichtete. Er erreichte Sterne bis V=24,1 mag [4]. Das ist
eine Größenklasse schwächer als die tiefsten Fotografien, die in der "Vor-CCD-Ära"
mit dem 5m-Hale-Teleskop gewonnen werden konnten!
Es ist also mit dieser Methode möglich in Bereiche vorzustoßen, die
mit einer Einzelbelichtung, durch die drohende Sättigung, unerreichbar
sind. Dies gelingt, weil vor dem Aufsummieren der Einzelbilder die
Detektorladung, verursacht durch den Hintergrund, abgezogen werden kann.
Andererseits muss jedoch betont werden, dass eine
lang belichtete Einzelaufnahme, gegenüber einer gleichlang gestückelten
Belichtung, aufgrund des geringeren Ausleserauschens, ein deutlich
besseres Signal-zu-Rausch-Verhältnis (sprich Reichweite) aufweist!
Leider lässt sich der ETC der ESO nicht zur exakten
Klärung dieses Sachverhaltes einsetzen. Die Aufnahmen von Wolfgang Düskau
(Bilder 1 und 2) demonstrieren aber eindrucksvoll den Reichweitengewinn
aufaddierter Einzelaufnahmen, der unter mäßigen Bedingungen aus einer Kleinstadt heraus mit nur 5 Zoll
Öffnung und CCD-Technik erzielbar ist. Die eingetragenen
Sternhelligkeiten geben nicht unbedingt den Intensitätseindruck der
ungefilterten Aufnahmen wieder.

Bild 1:
Ringnebel M 57 in der Leier, Aufnahme
von Wolfgang Düskau mit 5"-Refraktor, 1016 mm Brennweite (f/8), ohne
Filter, SBIG ST-7 CCD-Kamera, 30 Sekunden unter mäßigen
Beobachtungsbedingungen.

Bild 2:
Ringnebel M 57, Aufnahmedaten wie Bild
1, Belichtung 90x30 Sekunden über die Betriebsart "Traccum Accumulate"
aufaddiert. Zum Vergleich wurden die visuellen Helligkeiten einiger
umliegender Sterne (ohne Komma) eingefügt. Die Angaben wurden [5]
entnommen.
Schwächste Sterne und
Hintergrundhelligkeit
In der Fotografie mit klassischen hochempfindlichen
Emulsionen war es unmöglich Sterne abzubilden, die deutlich schwächer
waren als die Hintergrundhelligkeit. Sterne und Hintergrund addierten
sich dabei zu einer Schwärzung, die die winzigen Sternscheibchen vom
chaotischen Kornrauschen gerade noch abheben ließen. Die Tabelle 2
zeigt, welche Gesamthelligkeiten sternscheibchengroße Areale
Himmelshintergrund bei verschiedenen Brennweiten besitzen. Die
Winkelgrößen dieser Sternscheibchenareale sind auf eine Abbildung von
0,03 mm Ø bezogen und die Hintergrundhelligkeiten wurden
aus der
Optimalbedingung B = 22,7 mag/arcsec2 berechnet. Im Bereich "seeing-begrenzt"
und "adaptive Optik" steht der Winkeldurchmesser der
Sternscheibchenareale unabhängig von einer Brennweite.
Tabelle 2
(zur Erklärung
lies Text)
| Brennweite |
Winkeldurchmesser
schwächster
Sterne |
B-Helligkeit
in mag |
|
50 mm |
123,76" |
12,50 |
|
100 mm |
61,88" |
14,00 |
|
225 mm |
27,50" |
15,77 |
|
300 mm |
20,63" |
16,39 |
|
500 mm |
12,38" |
17,50 |
|
700 mm |
8,84" |
18,23 |
|
1000 mm |
6,19" |
19,00 |
|
2000 mm |
3,09" |
20,51 |
|
4000 mm |
1,55" |
22,01 |
|
6000 mm |
1,03" |
22,90 |
| seeing-begrenzt |
1,00" |
22,96 |
| |
0,65" |
23,90 |
| |
0,50" |
24,47 |
| |
0,30" |
25,58 |
| adaptive Optik |
0,10" |
27,96 |
Jedem Astrofotografen wird sofort ins Auge fallen, dass diese
Hintergrund-Helligkeitswerte den Sterngrenzgrößen ausbelichteter
Aufnahmen, gewonnen mit Instrumenten der aufgeführten Brennweiten,
auffällig nahe kommen. (Obwohl das unter ländlichen mitteleuropäischen
Bedingungen, wegen des deutlich helleren Hintergrundes, selbst mit einer
modernen Hochkontrastemulsion vom Typ eines TP 2415 und 0,02 mm
Sternscheibchen nur annähernd zu erreichen ist.)
Die Tabelle 2 suggeriert den Schluss, dass die Sterngrenzgrößen, aus
der Sicht ausbelichteter Fotografien über die Abbildungsmaßstäbe an die
Brennweite bzw. an die Winkelgrößen schwächster Sternscheibchen
gebunden sind [6]. Ausbelichtete, seeing-begrenzte
Fotografien sollten danach, trotz unterschiedlicher Instrumentengrößen,
eine einheitliche Grenzgröße nicht überschreiten können, da dies ein
tieferes Eindringen in den Hintergrund bedeutet.
Wie verhält sich das aber in der CCD-Astronomie?
Die Frage wird
dadurch verkompliziert, weil, wie die Diagramme 4b und 5 deutlich
machen, obige Überlegungen offenbar keine uneingeschränkte Gültigkeit
besitzen. Trotz gleichem Seeing enden dortige Kurven unterschiedlich,
was tatsächlich ein verschieden tiefes Eindringen in den Hintergrund
darstellt.
Aus den Diagrammen lässt sich ablesen, dass bei
gleicher Winkelgröße schwächster Sternscheibchen, im Sättigungsbereich
der Detektoren, die Grenzgrößen dann am höchsten liegen, wenn möglichst
lang belichtet werden muss, wenn das Öffnungsverhältnis klein und die
Detektorempfindlichkeit gering ist. Nach meiner Untersuchung
tragen zur Ursache die etwas unterschiedlichen Ladungssättigungswerte
der CCD-Detektoren (Diagramm 4b) nur wenig bei. Noch unbedeutender sind
die Unterschiede in den beleuchteten Pixelzahlen schwächster Sterne.
Primär kommen hierin zum einen die unterschiedlichen
Abbildungsgesetze von Punkt- und Flächenhelligkeiten zum Ausdruck, zum
anderen aber die Signal-zu-Rausch-Verhältnisse und die statistischen
Schwankungen der Photonenzahlen von Objekt und Hintergrund.
Bereits aus Formel (1) lässt sich in erster Näherung
ableiten, dass sich bei den gängigen Ladungssättigungswerten (Detector
saturation level) heutiger CCD-Detektoren nur etwa ein Hundertstel des
Himmelshintergrundes erreichen lässt. Tritt bei 100 000 registrierten
Photonen die Ladungssättigung (Objekt + Sky) ein, dann gilt etwa in
diesem Bereich für

ein Verhältnis von Stern zu Hintergrund 949 : 99051 = 1 : 104,37, was 5,05 mag
schwächer als ein entsprechend großes Stück Himmelshintergrund ist.
Die Fähigkeit tief in den Himmelshintergrund
einzudringen ist kein Privileg großer Teleskope. Neben dem
Öffnungsverhältnis, verwendeten Filtern und den oben geschilderten
S/N- und Quanteneinflüssen ist sie
primär eine Eigenschaft des Detektors
und wächst mit den Ladungssättigungswerten.
Je höher diese sind, umso tiefer gehen die Aufnahmen.
Spektroskopie und Reichweite
Weshalb unter irdischen Bedingungen auch der traditionelle
Einsatz immer größerer Optiken vorangetrieben wird, liegt hauptsächlich
an den Erfordernissen der Spektroskopie. Diesen Untersuchungsmethoden
verdankt die Astrophysik ihre wesentlichsten Erkenntnisse. Sehr schwache
Quellen lassen sich damit aber entweder gar nicht oder nur unter einem
unsäglichen Aufwand analysieren. Die Grenzgrößen sind gegenüber
Direktaufnahmen weit geringer (siehe auch Diagramm 1), da das zu
untersuchende Licht flächenmäßig aufgefächert werden muss. Der Wunsch
auch spektroskopisch immer tiefer vorzudringen, ist daher Hauptantrieb
für den Bau immer größerer bodengebundener Teleskope.
In der spaltlosen Spektroskopie
bleibt die Abbildungsintensität des flächenhaften Himmelshintergrundes,
entsprechend dem
Öffnungsverhältnis, unabhängig von der verwendeten Dispersion bestehen.
Lediglich die Lichtverluste durch die dispergierende Optik sind
abzurechnen. Die Grenzgrößen der Sternspektren werden ganz wesentlich
durch den Betrag der flächenmäßigen Verteilung des Sternlichtes
reduziert. Auch die spektrale Energieverteilung fließt hier ein,
wie auch der Umstand, dass die Empfindlichkeit des Detektors eine
Funktion der Wellenlänge ist.
Ein Spektrum ist also kein
gleichmäßig beleuchtetes Rechteck. Es soll aber an jeder Stelle
auswertbar sein. Daher ist ein S/N von 10 nicht zu unterschreiten, was
die Reichweiten zusätzlich drückt. Der Exposure Time Calculator der ESO
berechnet das S/N der Spektren für ihre zentrale Wellenlänge.
Um scharfe Spektren von
Flächenobjekten zu erhalten, aber auch zu Untersuchungen
mit hoher Dispersion von Punktquellen, benötigt man Spaltspektrographen.
Der Spalt legt die Größe und Position des Eingangsbildes genau
reproduzierbar fest. Dies ermöglicht, die Spektren in der gebotenen
Genauigkeit zu kalibrieren und wissenschaftlich auswertbar zu machen.
Da das Licht nur durch die
Fläche des Spalts eintreten kann, wird der darin enthaltene Anteil des
Himmelshintergrundes auf gleiche Weise auseinander gezogen und
geschwächt, wie der des Objektes. Diese starke Unterdrückung des
Hintergrundes ist ein weiterer wesentlicher Vorzug der
Spaltspektroskopie.
Es werden damit
riesige Belichtungszeiten möglich, aber zugleich auch nötig! Ein Grund
dafür liegt in der geringen Effizienz der Spaltspektrographen (Gitter).
Die instrumentellen Lichtverluste (Teleskop und Detektor) betragen
häufig über 80%! Hinzu kommt, dass das Licht eines Sterns, vor dem Spalt
szintillierend, oft teilweise weggeblendet wird. Sein Licht wird
geschwächt zugunsten des Hintergrundrauschens. Das Spektrum wird
breiter, flacher, seine Qualität sinkt.
Da große Teleskopöffnungen
Flächenhelligkeiten nicht verstärken,
deren Abbildungsintensität
resultiert ja hauptsächlich aus dem Öffnungsverhältnis,
sind zu deren
Untersuchung sowieso sehr lange Belichtungen erforderlich.
Der Vorteil
großer Teleskope liegt hier im Wesentlichen im Abbildungsmaßstab.
In der
Spektroskopie flächiger Objekte ist es von Bedeutung, benachbarte
Regionen gut voneinander trennen zu können. Dies gelingt natürlich mit
großen Instrumenten besser. Außerdem sind viele Flächenobjekte, vor
allem Galaxien, in gewissem Sinne "versteckte" Punktquellen. Diese
Untersuchungsobjekte, beispielsweise Kerne ferner Galaxien, unaufgelöste
Knoten, Jets, Sternhaufen ect. erfordern natürlich riesige Öffnungen.
Diagramm 6 zeigt, welche
Flächenhelligkeiten FORS 2 am 8,2m VLT mit Spektren von 5 nm/mm
Dispersion untersuchen kann (GRIS_600B, zentrale
Wellenlänge 470 nm, B-Band, Spaltbreite 0,51", Effizienz mit Extinktion
auf zentr. λ=13,59%, Binning 2x2, 11000K, Seeing 0,65", S/N=10).
Der Kurvenverlauf entspricht grundsätzlich dem von Diagramm 3. Durch die
Unterdrückung des Himmelshintergrundes und durch die geringe Effizienz
wird der Verlauf jedoch stark verlangsamt. Das Abstürzen der Kurve, im
Diagramm 3 Kriterium für den Bereich der Kurzbelichtung, geschieht hier
noch weit über praktikable Belichtungszeiten hinweg. Ursache dieses
Absturzes ist hauptsächlich der Hintergrundrauschanteil, der mit in den
Spalt eintreten kann. Aber
die Belichtungszeiten werden durch die
drohende Chipsättigung nicht limitiert.
Selbst am letzten Rechenpunkt,
nach fast 191 Stunden (Grenzgröße 26 mag/arcsec2), beträgt
die Detektorsättigung erst 32% (auf zentraler Wellenlänge)!
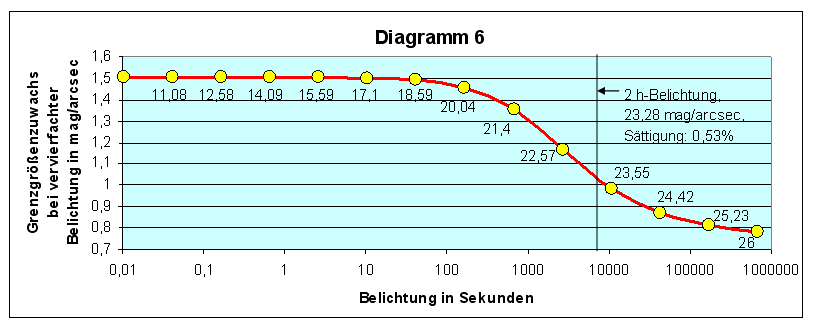
Diagramm 6:
Grenzgrößenzuwachs bei vervierfachten Belichtungszeiten in der
Spektroskopie flächenhafter Objekte, gültig für FORS 2 am 8,2m VLT und 5
nm/mm Dispersion (bestimmt mittels ETC)
Das Diagramm 7 ist ein Beispiel
für den Zusammenhang zwischen Öffnung und spektroskopischer Reichweite
bei Punktquellen. Verglichen wird FORS 2 (Einstellungen wie oben) und
EMMI (ESO Multi-Mode- Instrument) am Nasmyth
B-Fokus (f/11) des 3,6m NTT (Einstellungen: Gitter 5,
Dispersion 4,88 nm/mm, zentrale Wellenlänge 480 nm, B-Band, Spaltbreite
0,5", Effizienz mit Extinktion auf zentr. λ=10,43%, Binning 1x1, 11000K, Seeing
0,65", S/N=10).
Der Öffnungsflächenunterschied
beider Teleskope (1:5,753) schlägt sich, ähnlich den Diagrammen 4, nicht
unmittelbar im Grenzgrößenverlauf nieder. Bei einer Sekunde Belichtung
beträgt die Reichweitenüberlegenheit von FOES 2 noch das 4,52fache =
1,64 mag, bei 2stündiger Belichtung nur noch das 2,86fache = 1,14 mag,
und das, obwohl EMMI mit etwas höherer Dispersion, etwas schmalerem
Spalt, mit Binning 1x1, also mit geringerer Effizienz arbeitet! Dennoch
ist die Überlegenheit des 8,2m Teleskops signifikant.
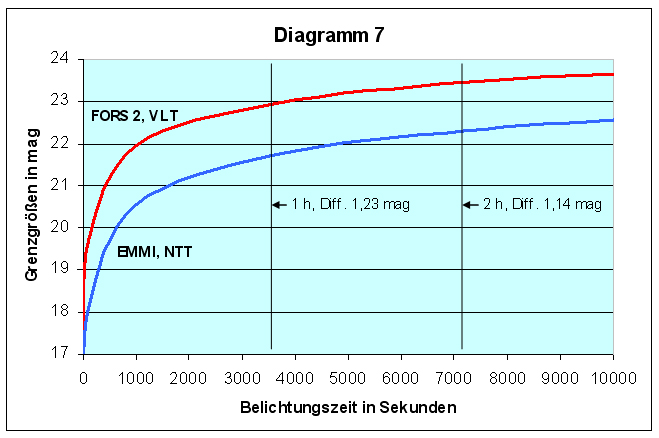
Diagramm 7:
Grenzgrößenzuwachs von Spektralaufnahmen (Punktquellen) mit FORS 2 (8,2m
VLT, 5 nm/mm Dispersion) und EMMI (3,6m
NTT, 4,88 nm/mm Dispersion). Die mit Pfeilen
markierten Linien kennzeichnen die Reichweite nach ein, bzw. 2 Stunden
Belichtung. Daneben die Grenzgrößendifferenz der Kurven. (Bestimmt
mittels ETC)
Ich möchte für wesentliche Hinweise vor allem Dr. Gero Rupprecht (ESO),
Dr. Susanne Friedrich, Dr. Thomas Rivinius (ESO),
dem Vds-Fachgruppenleiter "CCD-Technik" Dr. Dennis Möller, für Mitarbeit und Hilfe Wolfgang Düskau
und für Vermittlungsbemühungen dem Vds-Fachgruppenleiter "Spektroskopie" Ernst Pollmann
danken.
[1] ESO Optical Instrument Simulator, http://www.eso.org/observing/etc/doc/ut1/fors/helpfors.html
(Seite 2025 nicht mehr zu erreichen)
[2] Newberry, v. M.: The Signal to Noise
Connection, CCD-Astronomy, Sommer (1994)
[3] Kiesewetter, S.: 4 Kenndaten von FORS,
http://www.usm.uni-muenchen.de:8002/DO-CU/bmft/node4.html
(Seite 2025 nicht mehr zu erreichen)
[4] Schaefer, B. E.: Going to the Limit, Sky &
Telecope Vol. 97 Nr.5, 126 (1999)
[5] Skiff, B. A.: Taking Your Telescope to the
Limit, Sky & Telecope Vol. 102 Nr.9, 102 (2001)
[6]
Fischer, W.:
Die maximal erzielbaren Sterngrenzgrößen aus der Sicht des
Instrumentenvergleichs, Interstellarum 5, 60 (1995)

(Zähler, 09.2013)
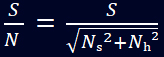 Vereinfacht bedeutet das nichts anderes als:
Vereinfacht bedeutet das nichts anderes als:
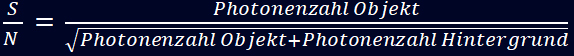 (1)
(1)










